
This old formulation method still has uses in commercial situations
Imagine being a farmer in some Midwestern state of the U.S. in the previous century, and you had only three ingredients to feed your animals: corn, soybean meal, and a supplement. The supplement contained nothing more than some vitamins; trace- and macro-minerals, including salt; perhaps a medication; and one or two other additives of no importance for this discussion. To make life easier, the nutrition supplier said you could use the supplement at 5% in all of your final feeds. The rest was up to you because that nutrition supplier wanted you to have freedom in making your rations.
For our discussion, we will assume you had to make four hog feeds: one for the young, one for the growers, one for gestating sows, and a final for lactating ones. Everything back then pivoted around protein, as lysine was not yet big news. So, the extension bulletin you had borrowed from the local library said these four feeds should have 18, 16, 14, and 12% crude protein, respectively. You check with your corn at harvest with your local extension service, and it came back at 9% crude protein (a good year), whereas your soybean meal dealer always sold it at 44% crude protein with a guaranteed analysis (a good dealer). By the way, your extension specialist was not available today, so you had to make your own feeds at the home farm’s office alone.
You start with the first feed, the one with 18% crude protein. You aced your algebra class at high school, and you know this is an easy enough problem with a=corn, b=soybean meal, and c=supplement percentage inclusion rates. We both make our teachers proud by writing down correctly the following equations:
(1) a+b+c=100
(2) 9a+44b+0c=18×100
As c=5 and crude protein in the supplement is zero, then the problem becomes even easier as follows:
(1) a+b=95
(2) 9a+44b=18×100
We said you aced algebra, so the solution is easy, but what if there were a more comfortable, faster and memorable way to solve this and any such similar problems? That’s where the Pearson Square method comes in to blend two ingredients with widely different compositions to provide a mix with an intermediate value. Here is how you construct one.
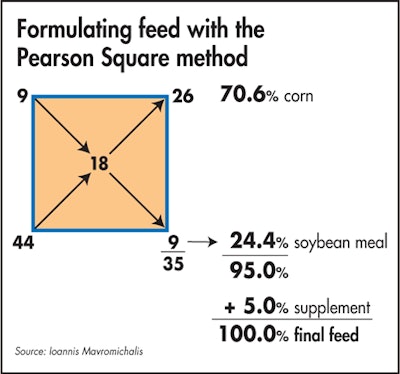
You draw a square and place the values for corn and soybean meal crude protein at the left upper and lower corners, respectively. In the middle, you write down the desired final mix crude protein concentration. Then, you deduct each two figures diagonally, always subtracting the smaller number from the larger one. So, for corn, it is 18-9=9; write that down the corner just across corn, as shown by the arrow. Next, for soybean meal, we have 44-18=26; again, write that down at the last corner, always following the arrows.
The two new numbers give you the parts of corn and soybean meal required to make a mix of the desired protein concentration. In our case, this is 9 parts soybean meal and 26 parts corn to get a total of 35 parts that contain 18% crude protein. Remembering that these parts make up 95% of our total feed, we divide each figure by 35 and multiply by 95 and we get 24.4% soybean meal and 70.6% corn giving 95%, plus 5% of the supplement, and we arrived at the grand total of 100%. Following the same procedure, we can easily calculate the proportions for all other feeds.
 This method allows nutritionists to blend two ingredients with widely different compositions.
This method allows nutritionists to blend two ingredients with widely different compositions.Modern uses
Today, the Pearson Square is not used as often as in the past. Some contemporary examples include a quick exchange from one soybean meal with 44% crude protein to another with higher crude protein, say 46%. That is, such an exchange is acceptable when a computer is not handy, and the animals must eat. It is also used in adjusting forage ration concentrations when one forage runs out, and another must be used in a rush. It is best to validate numbers later with a computer.
Some producers, especially smaller ones, still use one supplement, and a mix of corn and soybean meal. In this case, the supplement usually contains amino acids, and the producer is supplied with detailed directions on how to use it with the available grains. But, if the instructions fail to include all possible outcomes, then the Pearson Square can come handy if one knows the lysine or methionine (for pigs and poultry, respectively) levels in the supplement. These are usually shown on the supplement’s label. With this information, it is then easy to subtract the contributions from the supplement and readjust the cereal and protein source concentrations. Again, this is a last-measure method used in the field to account for emergencies.
An Excel spreadsheet can also be constructed to resolve these issues, and there is even an online calculator. But, if a computer is available, then a proper feed formulation program is also at hand, so adjustments can be appropriately made following the least-cost reformulation method. Still, the Pearson Square remains a great educational tool.















